
Figure 1. Plan view of the initial microtopography, scanned following 50 mm rainfall from a rainfall simulator
From a poster presented at the GCTE Soil Erosion Network Conference Global Change: Modelling Soil Erosion by Water at the Catchment Scale, University of Utrecht, The Netherlands, 14-18th April 1997.
David
Favis-Mortlock
*University of Oxford
Environmental Change Unit
5 South Parks Road
Oxford OX1 3UB
UK
*address when this was written
No currently existing model is capable of explicitly specifying the initial location and subsequent spatial development of hillslope rill systems in real landscapes. Without such a capability, models of soil erosion by water can produce only spatially generalised estimates of the whereabouts of erosion - and of its impacts - both under agriculture and under natural vegetation.
There is therefore a clear need for a modelling approach which is capable of an explicit spatial representation of the initiation and development of erosional systems. Such a model must:

Figure 1. Plan view of the initial microtopography, scanned following 50
mm rainfall from a rainfall simulator
This single-event model is able to generate apparently realistic rill networks (Figures 2 and 3). These are produced by the combined erosive action of many discrete runoff 'packets' moving on a grid of microtopographic elevations, derived either by laser scanning a soil pan or by stochastically computing a distribution of heights.

Figure 2(a). Plan view of the micro-rill/rill network, plus pools, generated
by the RillGrow model, after 50 iterations. Note that in Figures 2(a)
to (e), colours are assigned to rills on the basis of their relative (not absolute)
depths: thus similarly-coloured rills may well have very different depths in
different figures. Lighter blues indicate shallower pools
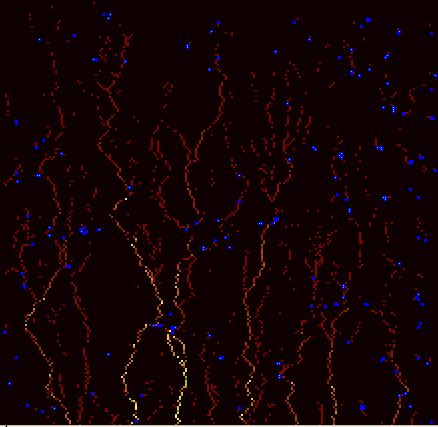
Figure 2(b). Network after 300 iterations

Figure 2(c). Network after 5000 iterations

Figure 2(d). Network after 100 000 iterations

Figure 2(e). Network after 10 000 000 iterations
Packet routing in the model is controlled only by microtopography. The majority of packets are small, and with an initial random position (i.e. produced by a single 'raindrop'). These flow down the line of steepest microtopographic gradient until they either leave the grid, or form or enter a pool in a microtopographic hollow. In the course of each simulation a smaller number of larger packets are also formed; these result from the overflow and breaching of pools. As each packet moves across the grid, it erodes the surface, using a streampower-based expression developed by Nearing et al. (1997).
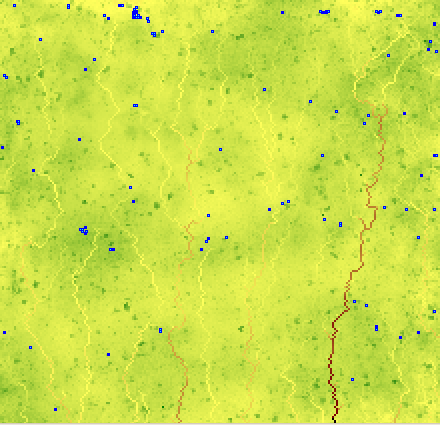
Figure 3. Plan view of microtopography, plus pools, after 10 000 000 iterations.
As in Figure 2, colours are assigned on the basis of relative (not absolute)
elevation; and lighter blues indicate shallower pools
Erosion thus lowers surface elevation, and so modifies the local microtopography; this in turn affects the routing of subsequent packets. The feedback loop so formed (Figure 4) enables the model to 'learn', i.e. to modify its subsequent behaviour based on past events. As a result the system 'evolves' i.e. displays self-organising, emergent behaviour.
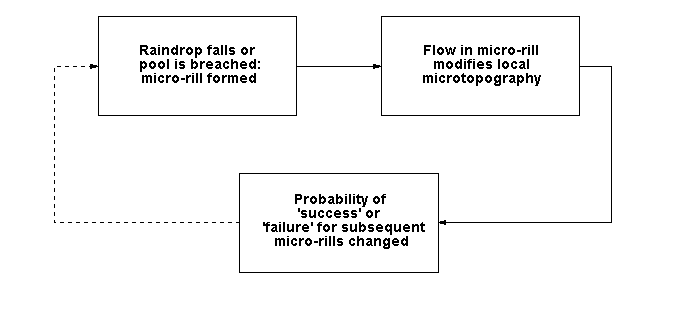
Figure 4. The RillGrow model's conceptual feedback loop (from Favis-Mortlock,
1996; 1998)
Thus the movement of runoff in the RillGrow model is governed by relatively simple rules (Table 1) acting upon microtopographic relief at a millimetre scale ('microscale'). The erosional features reproduced by the model are however on a scale of centimetres to metres ('macroscale').
| Rule | Description |
| 1 | Raindrops fall randomly on the cells making up the hillslope grid; the whole of each raindrop becomes a runoff 'packet'. One raindrop falls per iteration of the model |
| 2 | Runoff always tries to move to a lower adjacent cell down the steepest slope until it leaves the grid. If no adjoining cells are lower, the runoff stays where it is, forming (or adding to, if the cell is already wet) a pool |
| 3 | When runoff leaves a cell, it erodes it, thus lowering the elevation of that cell |
| 4 | If pools fill sufficiently, they breach. The water which overflows from the pool is routed to the next cell outside the breach and handled using rule 2, and so on |
Table 1. The rules used by the RillGrow model (from Favis-Mortlock, 1996; 1998)
As RillGrow models the movement of discrete packets of runoff on a grid according to a fixed set of rules, it may be thought of as a cellular automaton system. It differs from a conventional cellular automata system however, since the implementation of the rules governing automaton behaviour changes during the course of the simulation. In other words, although the rules themselves do not change, the outcome of their application for a given cell will depend on the past history of elevation change to this and adjacent cells. RillGrow may therefore be described as an 'evolving cellular automaton system'.
In addition to generating the networks shown in Figures 2 and 3, other realistic macroscale responses of the model include a narrowing of rill spacing with increased slope angle (Figure 5), an increased contribution of rill erosion with downslope distance (Figure 6), and a nonlinear increase of total erosion with slope steepness (Figure 7). Additionally, networks exhibit such features as an increase in rill depth below confluences, and micro-rill piracy (Figure 2: lower left). The microtopographic grid (Figure 3) shows a decrease in the correlation of cell-cell elevations, primarily at short correlation lengths (not illustrated here).
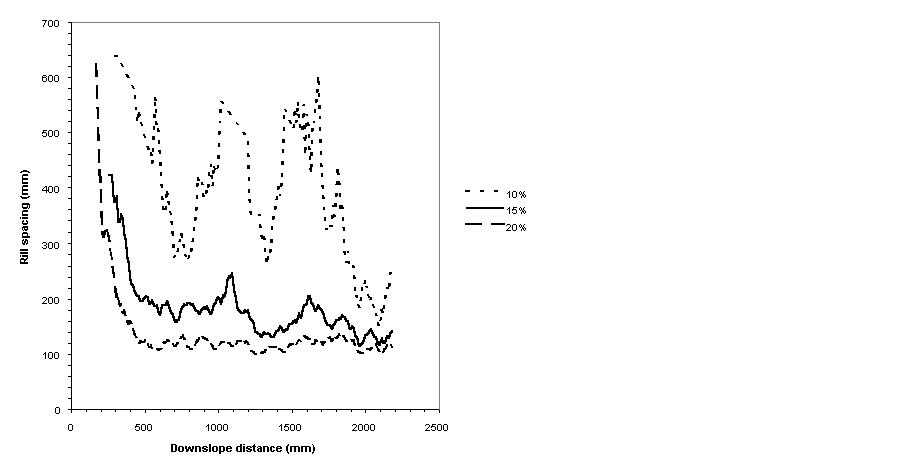
Figure 5. Simulated rill spacing for slope angles of 5, 10 and 15% (from
Favis-Mortlock, 1996; 1998)
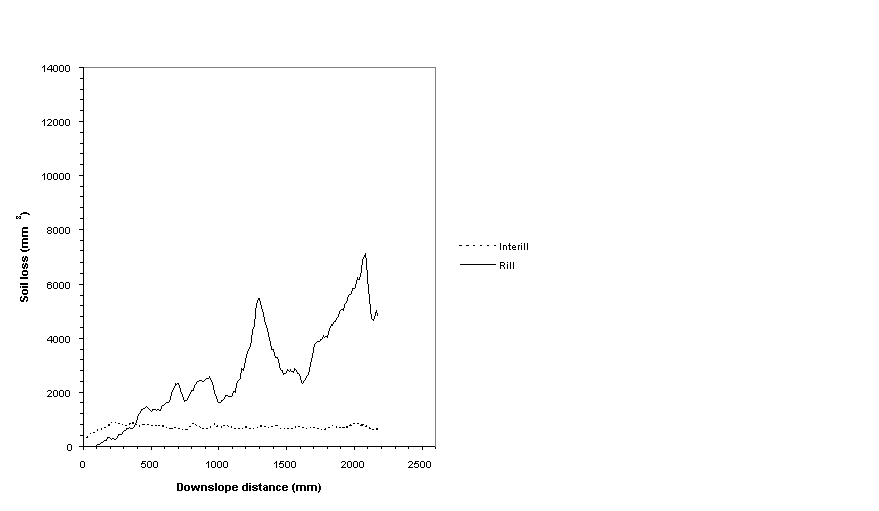
Figure 6. Simulated rill and inter-rill contributions on a 15% slope (from
Favis-Mortlock, 1996; 1998)
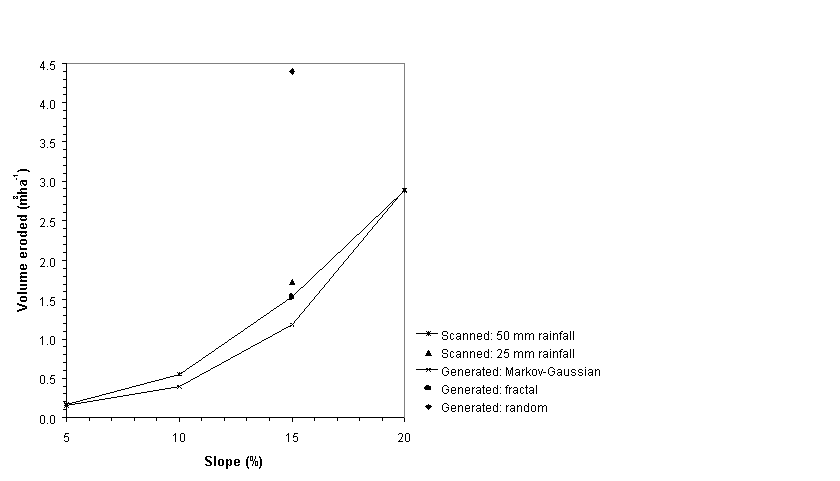
Figure 7. Total simulated erosion and slope angle for several initial microtopographic
distributions (from Favis-Mortlock, 1996; 1998)
Although the model produces very promising results, it has two main limitations. Firstly, in the current version, many process descriptions - e.g. infiltration - are omitted. Secondly the approach is very demanding of computational resources. This constrains the size of area to which it may be applied.
References
Favis-Mortlock, D.T. (1996). An evolutionary approach to the simulation of rill
initiation and development. In, Abrahart, R.J. (ed.), Proceedings of the
First International Conference on GeoComputation (Volume 1), School of Geography,
University of Leeds. pp. 248-281.
Favis-Mortlock, D.T. (1998). A self-organising dynamic systems approach to the simulation of rill initiation and development on hillslopes. Computers and Geosciences 24(4), 353-372.
Nearing, M.A., Norton, L.D., Bulgakov, D.A., Larionov, G.A., West, L.T. and Dontsova, K. (1997). Hydraulics and erosion in eroding rills. Water Resources Research 33(4), 865-876.